Practical applications ·

A Practical Guide to Seismic Flexible Retaining Wall Design

By Arun Kishore | 14 June 2025 | 7 minutes
A Practical Guide to Seismic Flexible Retaining Wall Design

So, you’ve just been handed a project with a decently sized retaining wall, and it’s in a location with some seismic kick. Immediately, you know that your standard static analysis isn’t going to cut it. The response of a retaining wall to seismic loading is a complex soil-structure interaction problem, and figuring out the right approach can be daunting.

For many of us, the first tool we reach for is the Mononobe-Okabe (M-O) method. It’s been the workhorse for seismic design of retaining structures for decades, first developed back in the 1920s and later simplified by Seed and Whitman in 1970. It’s a pseudo-static approach that extends the familiar static Coulomb wedge theory, making it relatively straightforward to apply.

But here’s the catch: while powerful, the M-O method isn’t a black box. It has some significant limitations you need to understand to use it correctly and safely. In this post, we’ll walk through the practical application of the M-O method for flexible retaining walls, focusing on what you as a Canadian engineer need to know. We’ll cover:

  • The core concept behind the M-O method.
  • How to determine your key seismic inputs using Canadian resources.
  • The critical limitations and “gotchas” that could trip you up.
  • How it all ties back to codes like the Canadian Highway Bridge Design Code (CHBDC).

A Quick Look at Mononobe-Okabe (M-O)

At its heart, the M-O method treats the seismic load as a static force. It calculates the total active thrust on the wall (\({P_{AE}}\)) during an earthquake by adding a dynamic component (\({\Delta P_{AE}}\)) to the static active thrust (\({P_A}\)).

$$P_{AE} = P_A + \Delta P_{AE}$$

Where,

$$P_A\ =\ \frac{1}{2}\ K_A\ *\ \gamma\ *\ H^2$$
$$ P_{AE}\ =\ \frac{1}{2} \ K_{AE}\ *\ \gamma\ *\ H^2\ *\ (1-k_v)$$
$$K_{\mathrm{A}}=\frac{\cos ^2(\phi-\theta)}{\cos ^2 \theta \ \cos (\delta+\theta)\left[1+\sqrt{\frac{\sin (\delta+\phi) \ \sin (\phi-\beta)}{\cos (\delta+\theta) \ \cos (\beta-\theta)}}\right]^2}$$
$$K_{\mathrm{AE}}=\frac{\cos ^2(\phi-\theta-\psi)}{\cos \psi \ \cos ^2 \theta \ \cos (\delta+\theta+\psi)\left[1+\sqrt{\frac{\sin (\delta+\phi) \ \sin (\phi-\beta-\psi)}{\cos (\delta+\theta+\psi) \ \cos (\beta-\theta)}}\right]^2}$$
  • \(\phi\) - soil angle of internal friction
  • \(\theta\) - slope of the back face of the retaining wall with vertical
  • \(\psi\) - \(tan{}^{-1}[k_h / (1-k_v)]\) = angle of the seismic coefficient
  • \(\beta\) - slope of the backfill with horizontal
  • \(\delta\) - angle of friction of the wall–backfill interface

This total thrust is a function of a dynamic active earth pressure coefficient, \({K_{AE}}\), the unit weight of the backfill, and the wall height. The math can look a little intense, but it’s really just accounting for the geometry of the wall and backfill, the soil properties, and the seismic shaking.

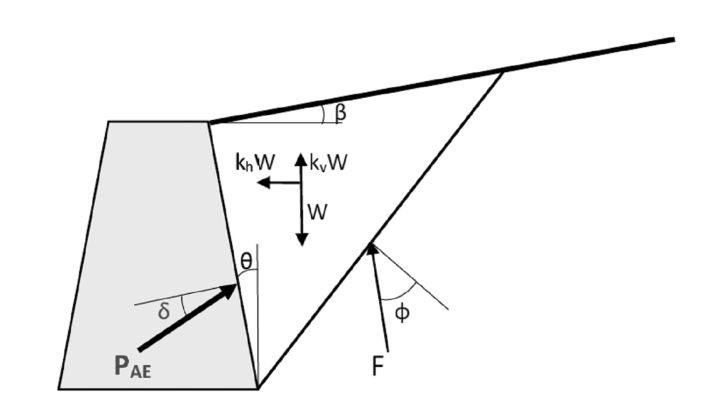Forces acting on a flexible retaining wall according to the Mononobe-Okabe pseudo-static method Forces acting on a flexible retaining wall according to the Mononobe-Okabe pseudo-static method. Source: Canadian Foundation Engineering Manual - 5th Edition

The goal is to find the total force (\({P_{AE}}\)) and where it acts on your wall so you can check for stability—sliding, overturning, and bearing capacity.

Nailing Down Your Seismic Coefficients (\({k_h}\) and \({k_v}\))

The most critical inputs for the M-O method are your seismic coefficients: \({k_h}\) for horizontal acceleration and \({k_v}\) for vertical.

The horizontal seismic coefficient, \({k_h}\), is defined as the ratio of the peak horizontal ground acceleration (\({a_h}\)) to gravity (g). For Canadian practice, you can get your site-specific Peak Ground Acceleration (PGA) directly from Natural Resources Canada’s online seismic hazard calculator for the NBCC 2020. You’ll need your site coordinates and the site class, which is determined from the soil conditions below the base of the wall, not including the backfill itself.

The vertical seismic coefficient, \({k_v}\), is often taken as a fraction of the horizontal one. In the absence of a site-specific assessment, a common rule of thumb is to assume \({k_v}\) is 2/3 of \({k_h}\).

Pro-Tip: Remember that the M-O method was developed for dry, cohesionless soils. If you have a saturated backfill, the calculations get more complex. The method needs to be modified to use the effective unit weight of the soil, and the angle of the seismic coefficient has to be adjusted based on the soil’s permeability.

Applying the Thrust: Where Does the Force Go?

Once you have the magnitude of the static (\({P_A}\)) and dynamic (\({\Delta P_{AE}}\)) thrusts, the next question is: where do they act?

  • The static component (\({P_A}\)) is typically applied at H/3 from the base of the wall.
  • The dynamic component (\({\Delta P_{AE}}\)) is often applied higher up. Seed and Whitman recommended applying it at 0.6H from the base.

The combined total active thrust (\({P_{AE}}\)) will therefore act somewhere between these two points. However, this is a point of some debate. More recent studies have suggested the application point might be closer to the static location, but this needs more verification before being adopted into standard practice. For now, sticking with the Seed and Whitman recommendation is a common and reasonably conservative approach.

Critical Limitations of the M-O Method

This is the part that separates a good design from a potentially failed one. The M-O method is powerful, but it comes with some serious caveats.

  • It’s for Flexible Walls: The method assumes the wall can deform enough (by sliding or rotating) to fully mobilize active earth pressure. It’s not appropriate for rigid walls that can’t move, like a basement wall braced by floor diaphragms. For those, you’d look at at-rest pressure methods.

  • It’s Not for Liquefiable Soils: The M-O method is fundamentally unsuitable for soils that could lose significant strength during an earthquake, such as through liquefaction. In fact, poor performance of retaining walls in past earthquakes has almost always been linked to liquefaction of the backfill or foundation soils. If you have liquefiable soils, M-O is off the table.

  • The Math Can Break: For certain combinations of steep backfill slopes, low soil friction angles, and high levels of shaking, the equation for the dynamic coefficient (\({K_{AE}}\)) can become indeterminate (you end up with the square root of a negative number). If this happens, it’s a sign that the assumptions of the method have been exceeded, and you need to switch to a different approach, like a limit equilibrium slope stability analysis.

Tying it to the Canadian Highway Bridge Design Code (CHBDC)

So, how does this fit into Canadian codes? The CHBDC provides some very practical guidance.

Key Takeaway from CHBDC: For retaining walls that are capable of deforming 25-50 mm, the CHBDC (CSA Group 2019) recommends you can design using \({k_h = 50\%}\) of the peak ground acceleration (\({a_h}\)) and you can set \({k_v = 0}\).

This is a huge practical consideration. It acknowledges that some permanent displacement is acceptable and even beneficial, as it limits the inertial forces the wall experiences. Allowing for this deformation can lead to a more economical and realistic design. It reflects a move towards performance-based principles, where we design for a certain level of acceptable movement rather than pure elastic resistance.

Final Thoughts

The Mononobe-Okabe method remains a cornerstone of seismic retaining wall design for a reason: it provides a rational, force-based approach that is well-understood. For flexible walls on sites with competent, non-liquefiable soils, it’s an excellent tool.

However, you have to respect its limits. Always check that your site conditions and wall type are appropriate for the method. When in doubt, or when dealing with critical structures, don’t hesitate to move to more advanced, performance-based methods like finite element analysis or Newmark sliding block analysis. These can give you a much better picture of how the wall will actually deform during an earthquake, which is ultimately what serviceability is all about.

What are your go-to methods or biggest challenges when designing retaining walls for seismic loads in Canada? Let’s discuss in the comments below.

Disclaimer: This blog post is for informational purposes only and should not be taken as specific engineering advice. Always consult the latest edition of the National Building Code of Canada and relevant CSA standards for your projects.