The “Why” Behind NBCC’s Snow Load Factors
- Deconstruct S = Is[Ss(CbCwCsCa)+Sr] so you can explain each lever to teams and AHJs.
- Know the origin stories—Cb’s surveys, Cw’s cautious reductions, Cs’s slope logic—to justify your selections.
- Show how combining the factors changes real roof load paths, especially on large or irregular plans.
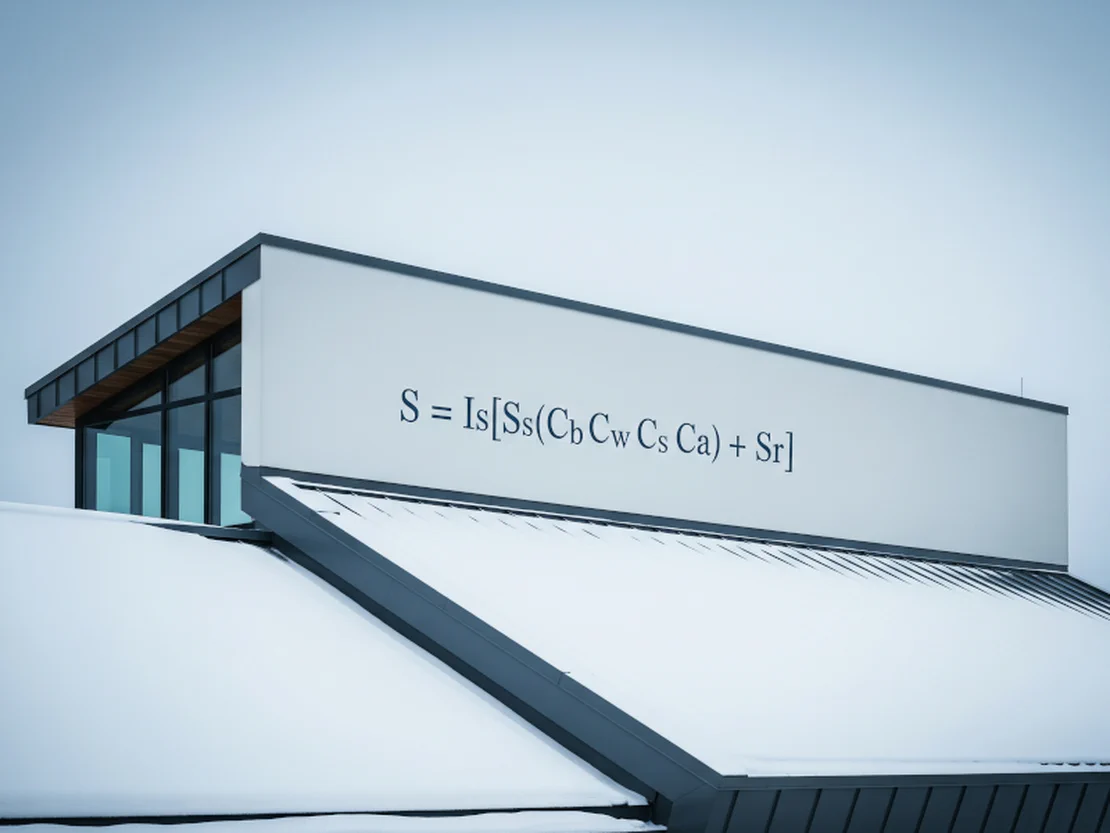
On this page
If you’re a structural engineer in Canada, you’ve stared at this equation more times than you can count:
$$S = I_s[S_s(C_b C_w C_s C_a) + S_r]$$It’s the backbone of our snow load calculations, a formula we trust to keep our buildings standing through the harshest Canadian winters. It’s important to remember this detailed formula is from NBCC Part 4; the approach for simpler structures is different, as we’ve covered in our guide to wind and snow loads in Part 4 vs. Part 9.
But have you ever stopped to think about the stories behind those factors? Why is the basic roof snow load factor, \(C_b\), usually 0.8? Why does it get more complicated for larger roofs? And why do we almost always end up using a wind exposure factor, \(C_w\), of 1.0, even when the code offers a reduction?
These aren’t just arbitrary numbers. They’re the product of decades of research, hard-won experience, and some fascinating engineering principles. So, let’s pull back the curtain and look at the “why” behind the numbers we use every day. It’ll not only make you a more well-rounded engineer but will also give you a deeper appreciation for the code we rely on.
Deconstructing the Master Formula
Before we dive into the individual factors, let’s do a quick refresher on the main equation from NBCC 2020 Article 4.1.6.2.
$$S = I_s[S_s(C_b C_w C_s C_a) + S_r]$$- \(S\) is our final specified snow load. It’s the load our roof needs to be designed for.
- \(I_s\) is the Importance Factor. This scales the load up for buildings where a failure would be catastrophic, and you can get a full breakdown by nailing down Importance Categories in NBC 2020.
- \(S_s\) is the 1-in-50-year ground snow load. This is our starting point, a baseline value for a specific location based on decades of climate data.
- \(S_r\) is the associated rain load. Because, of course, rain can fall on top of our snow, adding extra weight. For a deeper look at both \(S_s\) and \(S_r\), check out our structural engineer’s guide to the journey of snow.
- \(C_b, C_w, C_s, \text{ and } C_a\) are the modification factors that translate the ground snow load into a realistic roof load. These are where the real magic happens, and they’re what we’re going to focus on.
The Story Behind Cb = 0.8: A Cross-Country Survey
For many of the roofs we design, we start with a basic roof snow load factor, \(C_b\), of 0.8. This means we’re assuming the roof will see about 80% of the ground snow load. But where did that 20% reduction come from?
It wasn’t a guess. It’s rooted in one of the most significant undertakings in Canadian building science history. In the 1953 NBCC, the design snow load was simply equal to the ground snow load. This was safe, but often led to over-design. This is just one small part of the evolution of NBC structural design over the decades.
To get a more accurate picture, the NRC’s Division of Building Research (what is now the Construction Research Centre) launched a massive, country-wide survey of snow loads on roofs that ran from 1957 to 1968. With the help of volunteer observers across Canada, they gathered real-world data on how much snow actually accumulates on roofs compared to the ground.
The survey consistently showed that roof loads were, on average, less than ground loads. This makes sense when you think about it:
- Wind Scouring: Wind naturally blows snow off roofs.
- Melting and Sliding: Heat loss from the building and solar radiation can cause snow to melt, sublimate, or slide off, especially on sloped roofs.
Based on this mountain of data, the 1960 NBCC introduced the 80% rule, setting \(C_b\) at 0.8. It was a conservative simplification, but one grounded in extensive field observation.

A NRC researcher conducting a field observation as part of the 1957-1968 snow load survey. Source: NRCC - Snow loads for the design of roofs in Canada, Lutes, D.A.
Why Cb Increases for Larger Roofs
You’ve probably noticed that for larger roofs, the calculation for \(C_b\) gets more complex and often results in a value greater than 0.8. This change, introduced in the 2005 NBCC, accounts for the aerodynamic effects on large, open roof areas.
Think of it this way: on a small roof, the wind can effectively clear the snow. But on a large roof, the wind has a much longer “fetch.” It can pick up snow from one part of the roof and deposit it on another, creating drifts in areas of “aerodynamic shade.” The larger the roof, the more snow is available to be moved around, and the less effective the wind is at removing it from the roof entirely.
The formula for \(C_b\) on larger roofs is designed to capture this increased, non-uniform load. It recognizes that a large roof isn’t just a bigger version of a small roof; it behaves differently from an aerodynamic perspective.
The Cw Dilemma: To Reduce or Not to Reduce?
The wind exposure factor, \(C_w\), seems to offer a tempting reduction. The code allows us to reduce \(C_w\) to 0.75 in some cases, or even 0.5 for exposed sites north of the treeline. The logic is sound: a roof that’s fully exposed to the wind on all sides will have less snow accumulation.
So, why do most seasoned engineers almost always use \(C_w = 1.0\)?
In practice: The NBCC Commentary offers some crucial practical advice on this. It warns us to consider the probability of the roof becoming sheltered in the future by new buildings or even the growth of trees. The exposure conditions you see on site today might not be the conditions that exist 20, 30, or 50 years from now. Just as we must decode the wind commentary for its insights, the snow commentary is equally vital.
Given this uncertainty, the most prudent and common practice is to use \(C_w = 1.0\). It’s a conservative choice that ensures the building’s long-term safety, regardless of future developments on adjacent properties. Unless you’re dealing with a truly isolated building in a permanently open landscape, think very carefully before taking that reduction.
The Slope Factor (Cs)
Finally, let’s talk about the slope factor, \(C_s\). This one is perhaps the most intuitive. We all know that snow slides off sloped roofs. The \(C_s\) factor quantifies this effect, reducing the design load as the roof gets steeper. For a deeper look at the consequences of this, such as loads on lower roofs, our practical guide to snow loads on modern roofs is a great resource.
But the NBCC gets more nuanced than just the slope angle. It recognizes that the roof’s surface material plays a huge role. That’s why we have two different sets of criteria:
- “Unobstructed slippery roofs”: Think metal or glass. On these surfaces, snow slides off much more easily. The code allows for a load reduction starting at a slope of just 15°, and the load goes to zero at 60°.
- “Other” roofs: This covers most other common materials, like asphalt shingles, which have a higher coefficient of friction. For these, the load reduction doesn’t start until the slope hits 30°, and it doesn’t go to zero until 70°.
This distinction is based on the physics of friction and the creation of a meltwater layer at the snow-roof interface, which acts as a lubricant. It’s another example of how the code is built on a solid foundation of physical principles.
Bringing It All Together
The NBCC’s snow load equation isn’t just a formula; it’s a narrative. It tells the story of decades of Canadian research, of engineers learning from both successes and failures, and of a deep commitment to public safety.
By understanding the “why” behind factors like \(C_b\), \(C_w\), and \(C_s\), we move from being simple code-followers to knowledgeable practitioners. We can apply the code with more confidence, make more informed judgments, and better explain our design decisions to clients and colleagues.
So next time you’re deep in a snow load calculation, take a moment to appreciate the science and history packed into those simple-looking factors. They’re a testament to the ongoing evolution of our profession and the collective effort to build a safer Canada.
What are your thoughts or experiences with applying these factors in your projects? It’s often worth noting where you’ve chosen conservative assumptions like \(C_w = 1.0\) so future reviewers and clients understand the reasoning behind your snow load decisions.
Disclaimer: This blog post is for informational purposes only and should not be taken as specific engineering advice. Always consult the latest edition of the National Building Code of Canada and relevant CSA standards for your projects.
Next up for you
Standards, Design Principles, Practical Applications
A Structural Engineer's Guide to the Journey of Snow
A practical deep-dive for Canadian structural engineers into the nuances of snow loads, exploring the distinction between Ss and Sr, the …
Keep reading →Standards, Design Principles, Practical Applications
5 Live Load Nuances in the NBCC Commentary
A deep dive into five often-missed live load provisions in the NBCC 2020 commentary that every Canadian structural engineer should know, …
Keep reading →Standards, Design Principles, Practical Applications, Professional Development
Decoding the NBCC Wind Commentary
A practical walkthrough of the NBCC's Commentary on Wind Load and Effects, helping Canadian structural engineers navigate the three main …
Keep reading →Was this helpful?
Tell us what to cover next or request a deeper dive—every response goes straight to Arun.